Künstliche Intelligenz (KI) ist zurzeit in aller Munde und einer der größten Innovationstreiber in der IT-Branche. Viele denken KI sei noch in weiter Ferne, dabei befindet sich bereits heute in vielen Anwendungen ein Stück KI, z.B. in der Gesichtserkennung von beliebten Apps wie Snapchat oder Instagram. Fast ausnahmslos alle sozialen Netzwerke oder großen Tech-Portale wie Amazon setzen KI-Algorithmen um uns passende Vorschläge zu machen.
Da Mikrocontroller immer leistungsfähiger werden und in unserem Alltag an Bedeutung gewinnen, Stichwort IoT oder Wearables, ist es nur ein logischer Schritt dass die KI auch hier Einzug hält.
Bisher ist es so dass Mikrocontroller fest nach einem Schema Befehle abarbeit, d.h. der Programmierer hat den Ablauf formal spezifiziert, der Mikrocontroller bzw. die Software kann davon nicht abweichen. Kommt nun KI ins Spiel, ist die Verarbeitung zwischen Eingabe und Ausgabe der Daten nicht strikt festgelegt, sondern es werden wie beim Menschen Neuronen miteinander verbunden und dann mit Daten trainiert. Mit jedem Training wird das Ergebnis immer genauer.
Diesen Prozess nennt man auch Deep Learning (deutsch; mehrschichtiges Lernen). Natürlich werden keine echten Neuronen verwendet, sondern künstliche neuronale Netze (KNN), im Prinzip handelt es sich dabei um eine mathematische Struktur mit zahlreichen Zwischenlagen zwischen der Eingabe- und Ausgabeschicht.
Folgende Grafik soll dies verdeutlichen:

Dieser Beitrag soll jedoch nur die praktische Nutzung von Deep Learning aufzeigen, es ist nicht möglich hier auf Theorie einzugehen. Aus diesem Grund werden wir auch eine Software-Bibliothek verwenden, die uns in die Lage versetzen wird, Deep Learning relativ einfach auf einem Mikrocontroller einsetzen zu können.
Dieser Beitrag basiert auf dem Jupyter Notebook der TensorFlow Autoren (Apache License, Version 2.0).
DeepLearning Bibliothek TensorFlow Lite
TensorFlow Lite ist der „kleine Bruder“ von TensorFlow, ein quelloffenes Framework zur datenstromorientierten Programmierung, entwickelt von Google Brain Team.
An einem einfachen Beispiel werden wir Schritt für Schritt ein einfaches neuronales Modell erstellen und so trainieren, damit es in der Lage sein wird eine Sinus-Kurve nach zu ahmen.
Auf dem Mikrocontroller wird dieses künstliche neuronale Netzwerk mit Eingangsdaten „gefüttert“ (x-Koordinaten), dabei werden die Ausgangsdaten (y-Koordinaten) vorhergesagt (nicht berechnet!) und wir erhalten eine annähernd perfekte Sinus-Kurve ohne die mathematische Funktion y=sin(x) zu verwenden.
Zum Verständnis: Wir werden das Modell vorher am PC „per Hand“ entwickeln und trainieren, d.h. der Mikrocontroller erhält dann ein bereits trainiertes künstliches neuronales Netz. Ebenso werden die Eingangsdaten im Beispiel in der Software fest vorgegeben sein, nur die Ausgangsdaten bleiben natürlich offen. Auf diese Weise erhälst du ein grundlegendes Verständnis von diesem Thema ohne dich in der Komplexität zu verlieren.
In fortgeschrittenen Beispielen könnte man mit realen Sensordaten ein neuronales Netz auf einem Mikrocontroller trainieren, dann hätten wir tatsächlich ein System, das dynamisch auf die Umwelt reagiert und lernt. Nach diesem Tutorial könntest du dann in der Lage so ein System zu entwickeln.
Ein TensorFlow Modell erstellen
TensorFlow wird mit der Programmiersprache Python programmiert, Grundlagen reichen jedoch aus um die einzelnen Schritte nachvollziehen zu können.
Python-Abhängigkeiten importieren
Für unser Beispiel benötigen wir vier Python-Bibliotheken
- TensorFlow
- NumPy
- MatplotLib
- Math
Bitte richte dir deine Python-Umgebung so ein, dass du Zugriff auf diese Bibliotheken hast. Im folgenden Code werden die Bibliotheken eingebunden.
# TensorFlow is an open source machine learning library # Note: The following line is temporary to use v2 !pip install tensorflow==2.0.0-beta0 import tensorflow as tf # Numpy is a math library import numpy as np # Matplotlib is a graphing library import matplotlib.pyplot as plt # math is Python's math library import math
Trainingsdaten erzeugen
Damit wir später unser Modell trainieren können, müssen wir vorerst noch Trainingsdaten erzeugen, hier greifen wir auf die sin()-Funktion von Python zu. Ist das Modell trainiert, kann es bei Eingabe einer x-Koordinate die y-Koordinate vorhersagen!
Im nachfolgendem Code werden wir eine Reihe von x-Werten erzeugen und den Sinus davon berechnen.
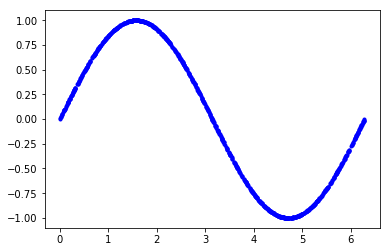
# We'll generate this many sample datapoints SAMPLES = 1000 # Set a "seed" value, so we get the same random numbers each time we run this # notebook np.random.seed(1337) # Generate a uniformly distributed set of random numbers in the range from # 0 to 2π, which covers a complete sine wave oscillation x_values = np.random.uniform(low=0, high=2*math.pi, size=SAMPLES) # Shuffle the values to guarantee they're not in order np.random.shuffle(x_values) # Calculate the corresponding sine values y_values = np.sin(x_values) # Plot our data. The 'b.' argument tells the library to print blue dots. plt.plot(x_values, y_values, 'b.') plt.show()
Für unsere Trainingsdaten erzeugen wir 1000 Werte (SAMPLES), die im Bereich von 2π liegen werden, also eine komplette Sinus-Welle. Sie werden in der Variablen x_values gespeichert. Danach werden die Werte mit der Funktion shuffle() durcheinander gewürfelt, damit sie nicht geordnet vorliegen. Anschließen werden die entsprechenden Sinus-Werte berechnet und in der Variablen y_values abgelegt.
Um eine Vorstellung von den Daten zu erhalten, werden wir sie über plot()-Funktion ausgeben.
Etwas Rauschen hinzufügen
Unsere Welt ist analog, daher wir unserer Sinuskurve, die wir mit der mathematischen sin()-Funktion erstellt haben, ein Rauschen hinzufügen. Auf diese Weise erhalten wir ein Modell, das sich mehr an unserer Realität orientiert.
Hast du schon mal eine Sinus-Kurve frei per Hand gezeichnet? Sie wird im mathematischen Sinne nicht perfekt sein, dennoch wird jeder sie als Sinus-Kurve erkennen, da unser Gehirn, d.h. unsere Neuronen perfekt darauf trainiert sind nicht so perfekte Gegenständlichkeiten unserer Umwelt wahrzunehmen. Und genau damit tun sich klassische Computer schwer.
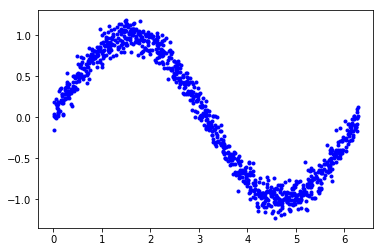
Im folgenden Code-Listing erzeugen wir mit der Zufallsfunktion randn() unsere verrauschten y-Werte.
# Add a small random number to each y value y_values += 0.1 * np.random.randn(*y_values.shape) # Plot our data plt.plot(x_values, y_values, 'b.') plt.show()
Um eine Vorstellung davon zu erhalten, plotten wir die verrauschten Werte.
Unsere Daten aufteilen
Mit diesen Daten werden wir unser Sinus-Modell trainieren. Um die Genauigkeit unseres Modells zu überprüfen, müssen wir die Vorhersagen mit unseren realen Daten vergleichen. Dieser Vergleich zwischen vorhergesagten Daten (engl. predictions) und realen Daten findet während des Trainings des Modells statt und nennt sich Validierung (engl. validation). Nach dem Training testen wir das Modell indem wir die vorhergesagten Daten mit Testdaten vergleichen (engl. testing).
Um dies zu erreichen, teilen wir unsere Daten in drei Bereiche auf:
- 60% der Daten zum Trainieren des Modells
- 20% der Daten zum Validieren
- 20% der Daten zum Testen
Diese Art der Aufteilung ist in der Praxis sehr üblich.
# We'll use 60% of our data for training and 20% for testing. The remaining 20% # will be used for validation. Calculate the indices of each section. TRAIN_SPLIT = int(0.6 * SAMPLES) TEST_SPLIT = int(0.2 * SAMPLES + TRAIN_SPLIT) # Use np.split to chop our data into three parts. # The second argument to np.split is an array of indices where the data will be # split. We provide two indices, so the data will be divided into three chunks. x_train, x_test, x_validate = np.split(x_values, [TRAIN_SPLIT, TEST_SPLIT]) y_train, y_test, y_validate = np.split(y_values, [TRAIN_SPLIT, TEST_SPLIT]) # Double check that our splits add up correctly assert (x_train.size + x_validate.size + x_test.size) == SAMPLES # Plot the data in each partition in different colors: plt.plot(x_train, y_train, 'b.', label="Train") plt.plot(x_test, y_test, 'r.', label="Test") plt.plot(x_validate, y_validate, 'y.', label="Validate") plt.legend() plt.show()
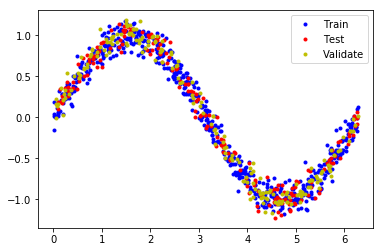
Die Aufteilung der Daten wurden zur Veranschaulichung farblich hervorgehoben. Die Daten wurden nicht verändert, sondern nur unterschiedlichen Variablen zugeordnet, nämlich
- x_train bzw. y_train (blaue Punkte)
- x_validate bzw. y_validate (gelbe Punkte)
- x_test bzw. y_test (rote Punkte)
Und so sieht die Grafik aus:
Unser Modell designen
Bis jetzt haben wir nur Daten erzeugt, jetzt beginnen wir mit dem Design des Modells. Und zwar soll das Modell bei gegebenen x-Werten die y-Werte vorhersagen. Dabei verwenden wir die mathematische Methode der Regression oder Regressionsanalyse. Dabei wird zwischen einer oder mehreren unabhängigen Variablen (unser x-Wert) und einer abhängigen Variable (unser y-Wert) eine Beziehung modelliert.
Um dies zu erreichen erstellen wir ein einfaches künstliches neuronales Netzwerk, die auf einer Regression Loss Function basieren wird. Leider kann ich nicht näher darauf eingehen und verweise auf entsprechende Literatur, z.B. diesen englischsprachigen Online-Beitrag
5 Regression Loss Functions All Machine Learners Should Know
Hier folgt das Code-Listing um unser Modell zu erzeugen.
# We'll use Keras to create a simple model architecture from tensorflow.keras import layers model_1 = tf.keras.Sequential() # First layer takes a scalar input and feeds it through 16 "neurons". The # neurons decide whether to activate based on the 'relu' activation function. model_1.add(layers.Dense(16, activation='relu', input_shape=(1,))) # Final layer is a single neuron, since we want to output a single value model_1.add(layers.Dense(1)) # Compile the model using a standard optimizer and loss function for regression model_1.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
Zur Erläuterung:
model_1 ist unser TensorFlow Modell. Diesem fügen wir eine Schicht (engl. layer) mit 16 „Neuronen“ hinzu. Die abschließende Schicht besteht nur aus einem Neuron, der unseren Ausgabewert liefern wird.
Die Funktion compile() kompiliert unser Model, dabei wird ein Standard-Optimierer „rmsprop“ und die Regressionsfunktion „mse“ als Parameter übergeben.
Nun ist es soweit: Wir trainieren unser Modell
Wir haben unsere Daten und wir haben unser Modell. Nun können wir mit dem Training des künstlichen neuronalen Netzwerks beginnen.
Was passiert genau beim Training?
Wir übergeben aus unseren Trainingsdaten einen x-Wert an das neuronale Netzwerk und überprüfen inwieweit der Ausgabewert vom erwarteten Wert abweicht. Je nach Größe der Abweichung werden die Gewichtung (engl. weights) und Verzerrrung (engl. bias) der Neuronen angepasst, so dass unser Ausgabewert beim nächsten Durchlauf etwas mehr unserem Erwartungswert entsprechen wird.
Dieser Prozess wird mehrmals durchlaufen. Man spricht auch von einer Epoche (engl. epoch) wenn das komplette neuronale Netz einmal durchlaufen wurde.
Der folgende Code trainiert unser Netzwerk, dabei werden insgesamt 1000 Epochen durchlaufen.
# Train the model on our training data while validating on our validation set history_1 = model_1.fit(x_train, y_train, epochs=1000, batch_size=16, validation_data=(x_validate, y_validate))
Für das Training ist die Funktion fit() zuständig. Pro Epoche übergeben wir nicht alle x- und y-Werte sondern einen Stapel von 16 Werten (batch_size). Als weiteren Parameter übergeben wir unsere Validierungsdaten.
Das Ergebnis sieht dann gekürzt wie folgt aus:
Train on 600 samples, validate on 200 samples Epoch 1/1000 600/600 [==============================] - 0s 412us/sample - loss: 0.5016 - mae: 0.6297 - val_loss: 0.4922 - val_mae: 0.6235 Epoch 2/1000 600/600 [==============================] - 0s 105us/sample - loss: 0.3905 - mae: 0.5436 - val_loss: 0.4262 - val_mae: 0.5641 ... Epoch 998/1000 600/600 [==============================] - 0s 109us/sample - loss: 0.1535 - mae: 0.3068 - val_loss: 0.1507 - val_mae: 0.3113 Epoch 999/1000 600/600 [==============================] - 0s 100us/sample - loss: 0.1545 - mae: 0.3077 - val_loss: 0.1499 - val_mae: 0.3103 Epoch 1000/1000 600/600 [==============================] - 0s 132us/sample - loss: 0.1530 - mae: 0.3045 - val_loss: 0.1542 - val_mae: 0.3143
Wir wollen uns die Metriken loss und val_loss genauer anschauen und auf die Bedeutung eingehen um das Ergebnis beurteilen zu können.
Die Metriken aus dem Training überprüfen
Die Distanz zwischen vorhergesagten und realen Daten wird als Trainingsverlust bezeichnet (engl. training loss).
-> Metrik loss
Die Distanz zu den Validierungsdaten wird als Validierungsverlust bezeichnet (engl. validation loss).
-> Metrik val_loss
Für eine bessere Vorstellung werden wir die beiden Metriken in einer Grafik darstellen. Dazu nutzen wir wieder ein kleines Python-Programm.
# Draw a graph of the loss, which is the distance between # the predicted and actual values during training and validation. loss = history_1.history['loss'] val_loss = history_1.history['val_loss'] epochs = range(1, len(loss) + 1) plt.plot(epochs, loss, 'g.', label='Training loss') plt.plot(epochs, val_loss, 'b', label='Validation loss') plt.title('Training and validation loss') plt.xlabel('Epochs') plt.ylabel('Loss') plt.legend() plt.show()
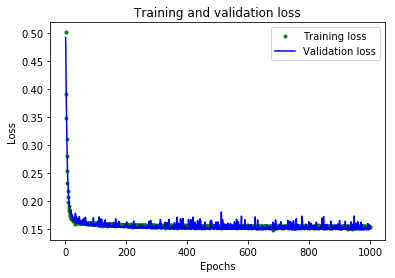
Wenn wir die Verluste in Abhängigkeit der Epochen darstellen, können wir sehr schön erkennen, dass die Verluste am Anfang ziemlich hoch sind, aber dann sehr schnell abfallen.
Nach 1000 Epochen hat sich das ganze in etwa bei 0.15 eingependelt.
Aber was passiert wenn wir in das neuronale Netzwerk noch eine Schicht einbauen? Du kannst es dir denken, dass wir dann mit einem besseren Ergebnis rechnen können. Lass es uns ausprobieren.
Mehr Neuronen für unser Modell
Aktuell verfügt unser Modell über zwei Schichten: die erste Schicht mit 16 Neuronen und die letzte Schicht mit einem Neuron für die Ausgabe des vorhergesagten Wertes. Zwischen beiden Schichten werden wir nun eine weitere Schicht mit 16 Schichten einfügen.
model_2 = tf.keras.Sequential() # First layer takes a scalar input and feeds it through 16 "neurons". The # neurons decide whether to activate based on the 'relu' activation function. model_2.add(layers.Dense(16, activation='relu', input_shape=(1,))) # The new second layer may help the network learn more complex representations model_2.add(layers.Dense(16, activation='relu')) # Final layer is a single neuron, since we want to output a single value model_2.add(layers.Dense(1)) # Compile the model using a standard optimizer and loss function for regression model_2.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
Nun durchlaufen wir wieder den gleichen Prozess wie oben. Die Validierungsverluste sind nun ein Zehntel kleiner, sie liegen also bei 0.015. Das ist ein sehr guter Wert, dabei haben wir nur eine weitere Schicht eingefügt.
Wer möchte, kann nicht natürlich gerne weitere Schichten einfügen.
Unser Modell zu TensorFlow Lite konvertieren
Da unser Modell nun brauchbare Ergebnisse liefert, ist es an der Zeit unser Modell in ein Format zu übertragen, dass nur wenig Speicherplatz benötigt und leicht von einem Mikrocontroller verwendet werden kann.
Dazu verwenden wir den TensorFlow Lite Converter. Hier folgt das Python-Programm.
# Convert the model to the TensorFlow Lite format without quantization converter = tf.lite.TFLiteConverter.from_keras_model(model_2) tflite_model = converter.convert() # Save the model to disk open("sine_model.tflite", "wb").write(tflite_model) # Convert the model to the TensorFlow Lite format with quantization converter = tf.lite.TFLiteConverter.from_keras_model(model_2) converter.optimizations = [tf.lite.Optimize.OPTIMIZE_FOR_SIZE] tflite_model = converter.convert() # Save the model to disk open("sine_model_quantized.tflite", "wb").write(tflite_model)
Das Ergebnis ist eine Datei mit dem Namen sine_model_quantized.tflite. Diese Datei können wir jedoch noch nicht in ein Arduino-Programm einbauen, wir müssen sie vorher noch in eine C-Quellcodedatei umwandeln. Dies erfolgt über die Kommandozeile mit dem Tool xxd.
# Install xxd if it is not available apt-get -qq install xxd # Save the file as a C source file xxd -i sine_model_quantized.tflite > sine_model_quantized.cc # Print the source file cat sine_model_quantized.cc
Als Ergebnis erhalten wir die Datei sine_model_quantized.cc.
Einbau unseres Modells in ein Arduino-Beispielprogramm
Das Beispielprogramm ist Teil der offiziellen TensorFlow Lite Arduino Bibliothek. Um es zu installieren, musst du den Bibliotheksmanager Tools -> Manage Libraries… in der Arduino IDE öffnen und nach Arduino_TensorFlowLite suchen und laden.
Unter File -> Examples wirst du nun das Beispiel TensorFlowLite:hello_world (Github) finden. Das Programm lässt die eingebaute LED deines Arduino Boards blinken, die Helligkeit der LED ist dabei abhängig vom y-Wert.
Hinweis: Um die Helligkeit der built-in LED zu steuern, wird PWM verwendet. Nicht jedes Board hat eine built-in LED mit PWM Funktionalität, in diesem Fall wird die LED einfach nur blinken.
Natürlich kannst du das Programm so anpassen, damit die Werte über ein Display grafisch dargestellt werden. Oder du nutzt den Arduino Plotter, der sich über Tools -> Serial Plotter aufrufen lässt, um den Verlauf auf deinem Rechner darstellen zu lassen.
Das Programm wurde mit folgenden Boards getestet:
- Arduino Nano 33 BLE Sense
- Arduino MKRZERO
Hast du Fragen? Dann schreibe mir bitte einen Kommentar, ich helfe gerne weiter.